This function computes variable contributions for individual predictions using the Shapley values, a method from cooperative game theory where the variable values of an observation work together to achieve the prediction. In addition, to make variable contributions easily explainable, the function decomposes the entire model R-Squared (R2 or the coefficient of determination) into variable-level attributions of the variance (Redell, 2019).
getShapleyR2(
object,
newdata,
newoutcome = NULL,
thr = NULL,
ncores = 2,
verbose = FALSE,
...
)Arguments
- object
A model fitting object from
SEMml(),SEMdnn()orSEMrun()functions.- newdata
A matrix containing new data with rows corresponding to subjects, and columns to variables.
- newoutcome
A new character vector (as.factor) of labels for a categorical output (target)(default = NULL).
- thr
A numeric value [0-1] indicating the threshold to apply to the signed Shapley R2 to color the graph. If thr = NULL (default), the threshold is set to thr = 0.5*max(abs(signed Shapley R2 values)).
- ncores
number of cpu cores (default = 2)
- verbose
A logical value. If FALSE (default), the processed graph will not be plotted to screen.
- ...
Currently ignored.
Value
A list od four object: (i) shapx: the list of individual Shapley values of predictors variables per each response variable; (ii) est: a data.frame including the connections together with their signed Shapley R-squred values; (iii) gest: if the outcome vector is given, a data.frame of signed Shapley R-squred values per outcome levels; and (iv) dag: DAG with colored edges/nodes. If abs(sign_r2) > thr and sign_r2 < 0, the edge is inhibited and it is highlighted in blue; otherwise, if abs(sign_r2) > thr and sign_r2 > 0, the edge is activated and it is highlighted in red. If the outcome vector is given, nodes with absolute connection weights summed over the outcome levels, i.e. sum(abs(sign_r2[outcome levels])) > thr, will be highlighted in pink.
Details
Lundberg & Lee (2017) proposed a unified approach to both local explainability (the variable contribution of a single variable within a single sample) and global explainability (the variable contribution of the entire model) by applying the fair distribution of payoffs principles from game theory put forth by Shapley (1953). Now called SHAP (SHapley Additive exPlanations), this suggested framework explains predictions of ML models, where input variables take the place of players, and their contribution to a particular prediction is measured using Shapley values. Successively, Redell (2019) presented a metric that combines the additive property of Shapley values with the robustness of the R-squared (R2) of Gelman (2018) to produce a variance decomposition that accurately captures the contribution of each variable to the explanatory power of the model. We also use the signed R2, in order to denote the regulation of connections in line with a linear SEM, since the edges in the DAG indicate node regulation (activation, if positive; inhibition, if negative). This has been recovered for each edge using sign(beta), i.e., the sign of the coefficient estimates from a linear model (lm) fitting of the output node on the input nodes, as suggested by Joseph (2019). Additionally, in order to ascertain the local significance of node regulation with respect to the DAG, the Shapley decomposition of the R-squared values for each outcome node (r=1,...,R) can be computed by summing the ShapleyR2 indices of their input nodes. Finally, It should be noted that the operations required to compute kernel SHAP values are inherently time-consuming, with the computational time increasing in proportion to the number of predictor variables and the number of observations. Therefore, the function uses a progress bar to check the progress of the kernel SHAP evaluation per observation.
References
Shapley, L. (1953) A Value for n-Person Games. In: Kuhn, H. and Tucker, A., Eds., Contributions to the Theory of Games II, Princeton University Press, Princeton, 307-317.
Scott M. Lundberg, Su-In Lee. (2017). A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS'17). Curran Associates Inc., Red Hook, NY, USA, 4768–4777.
Redell, N. (2019). Shapley Decomposition of R-Squared in Machine Learning Models. arXiv: Methodology.
Gelman, A., Goodrich, B., Gabry, J., & Vehtari, A. (2019). R-squared for Bayesian Regression Models. The American Statistician, 73(3), 307–309.
Joseph, A. Parametric inference with universal function approximators (2019). Bank of England working papers 784, Bank of England, revised 22 Jul 2020.
Examples
# \donttest{
# load ALS data
ig<- alsData$graph
data<- alsData$exprs
data<- transformData(data)$data
#> Conducting the nonparanormal transformation via shrunkun ECDF...done.
#...with train-test (0.5-0.5) samples
set.seed(123)
train<- sample(1:nrow(data), 0.5*nrow(data))
rf0<- SEMml(ig, data[train, ], algo="rf")
#> Running SEM model via ML...
#> done.
#>
#> RF solver ended normally after 23 iterations
#>
#> logL:-33.16687 srmr:0.086188
res<- getShapleyR2(rf0, data[-train, ], thr=NULL, verbose=TRUE)
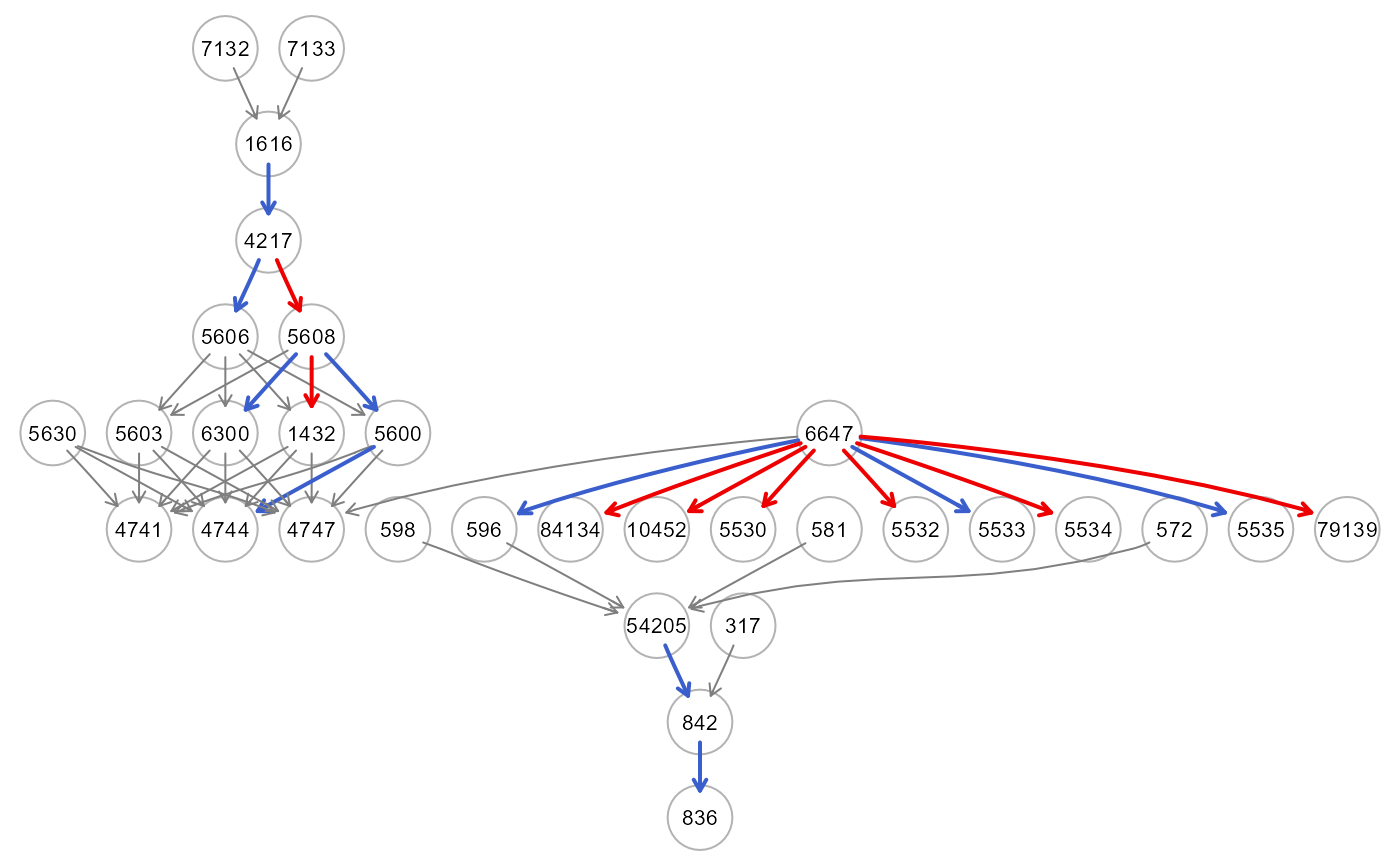table(E(res$dag)$color)
#>
#> gray50 red2 royalblue3
#> 32 7 6
# shapley R2 per response variables
R2<- abs(res$est[,4])
Y<- res$est[,1]
R2Y<- aggregate(R2~Y,data=data.frame(R2,Y),FUN="sum");R2Y
#> Y R2
#> 1 10452 0.3074106
#> 2 1432 0.2746912
#> 3 1616 0.1025127
#> 4 4217 0.2416770
#> 5 4741 0.2133041
#> 6 4744 0.2336151
#> 7 4747 0.3015739
#> 8 54205 0.2243528
#> 9 5530 0.4424930
#> 10 5532 0.3852137
#> 11 5533 0.3368840
#> 12 5534 0.4944426
#> 13 5535 0.5919868
#> 14 5600 0.2887038
#> 15 5603 0.0000000
#> 16 5606 0.2963567
#> 17 5608 0.5054904
#> 18 596 0.2057984
#> 19 6300 0.3769140
#> 20 79139 0.4867639
#> 21 836 0.5841519
#> 22 84134 0.4718743
#> 23 842 0.3401094
r2<- mean(R2Y$R2);r2
#> [1] 0.3350574
# }