The function computes a formal test for the significance of neural network input nodes, based on a linear relationship between the observed output and the predicted values of an input variable, when all other input variables are maintained at their mean values, as proposed by Mohammadi (2018).
getInputPvalue(object, thr = NULL, verbose = FALSE, ...)Arguments
- object
A neural network object from
SEMdnn()function.- thr
A value of the threshold to apply to input p-values. If thr=NULL (default), the threshold is set to thr=0.05.
- verbose
A logical value. If FALSE (default), the processed graph will not be plotted to screen.
- ...
Currently ignored.
Value
A list od two object: (i) a data.frame including the connections together with their p-values, and (ii) the DAG with colored edges. If p-values > thr and t-test < 0, the edge is inhibited and it is highlighted in blue; otherwise, if p-values > thr and t-test > 0, the edge is activated and it is highlighted in red.
Details
A neural network with an arbitrary architecture is trained, taking into account factors like the number of neurons, hidden layers, and activation function. Then, network's output is simulated to get the predicted values of the output variable, fixing all the inputs (with the exception of one nonconstant input variable) at their mean values; network’s predictions are saved, after doing this for each input variable. As last step, multiple regression analysis is applied node-wise (mapping the input DAG) on the observed output nodes with the predicted values of the input nodes as explanatory variables. The statistical significance of the coefficients is evaluated with the standard t-student critical values, which represent the importance of the input variables.
References
S. Mohammadi. A new test for the significance of neural network inputs. Neurocomputing 2018; 273: 304-322.
Examples
# \donttest{
if (torch::torch_is_installed()){
# load ALS data
ig<- alsData$graph
data<- alsData$exprs
data<- transformData(data)$data
dnn0 <- SEMdnn(ig, data, train=1:nrow(data), cowt = FALSE,
#loss = "mse", hidden = 5*K, link = "selu",
loss = "mse", hidden = c(10, 10, 10), link = "selu",
validation = 0, bias = TRUE, lr = 0.01,
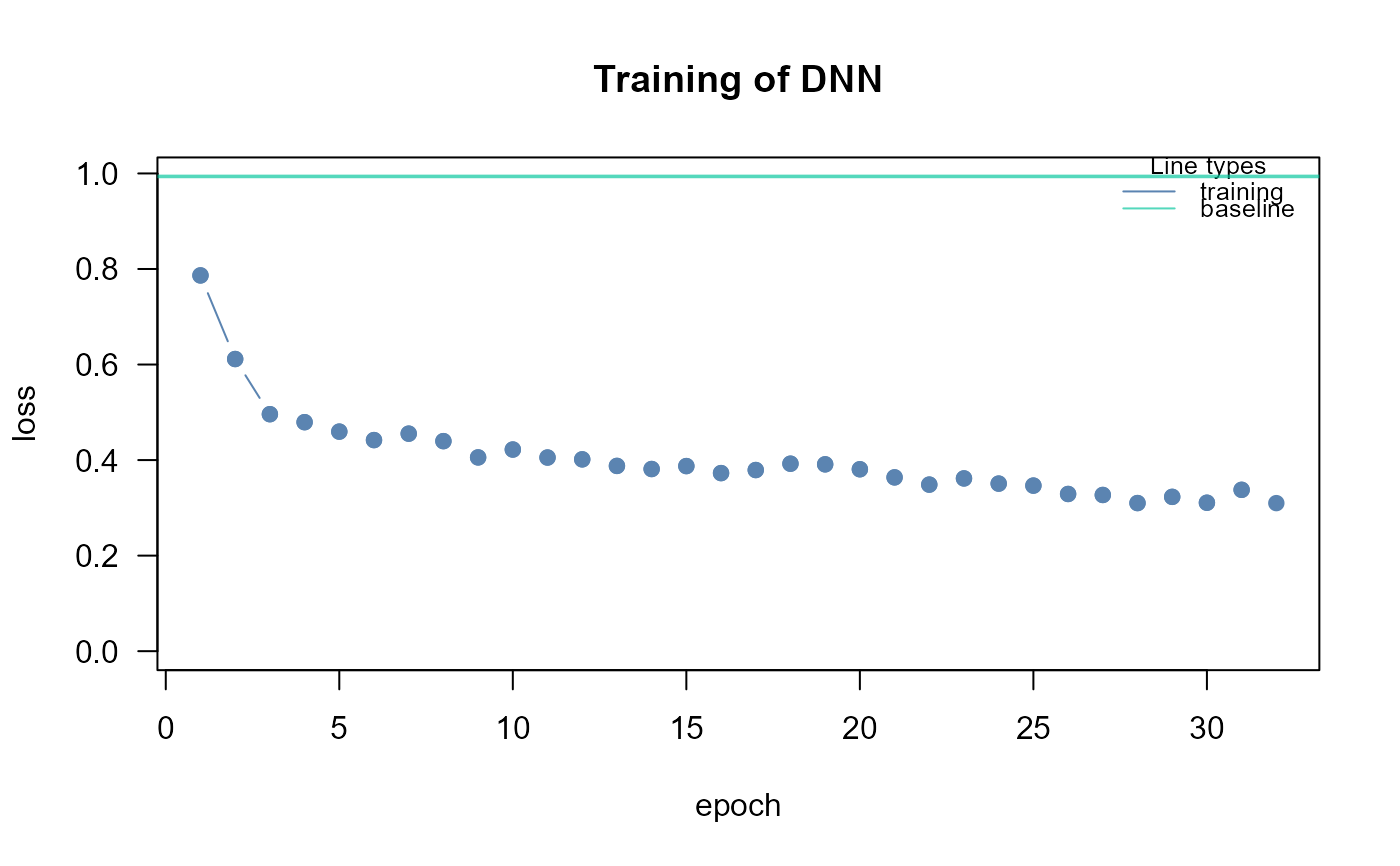
epochs = 32, device = "cpu", verbose = TRUE)
res<- getInputPvalue(dnn0, thr=NULL, verbose=TRUE)
table(E(res$dag)$color)
}
#> Conducting the nonparanormal transformation via shrunkun ECDF...done.
#> 1 : z10452 z84134 z836 z4747 z4741 z4744 z79139 z5530 z5532 z5533 z5534 z5535
#>
#> epoch train_l valid_l
#> 32 32 0.2688539 NA
#>
#> 2 : z842 z1432 z5600 z5603 z6300
#>
 #> epoch train_l valid_l
#> 32 32 0.3309115 NA
#>
#> 3 : z54205 z5606 z5608
#>
#> epoch train_l valid_l
#> 32 32 0.3309115 NA
#>
#> 3 : z54205 z5606 z5608
#>
 #> epoch train_l valid_l
#> 32 32 0.2966749 NA
#>
#> 4 : z596 z4217
#>
#> epoch train_l valid_l
#> 32 32 0.2966749 NA
#>
#> 4 : z596 z4217
#>
 #> epoch train_l valid_l
#> 32 32 0.390165 NA
#>
#> 5 : z1616
#>
#> epoch train_l valid_l
#> 32 32 0.390165 NA
#>
#> 5 : z1616
#>
 #> epoch train_l valid_l
#> 32 32 0.2757614 NA
#>
#>
#> DNN solver ended normally after 736 iterations
#>
#> logL:-43.177633 srmr:0.101807
#> epoch train_l valid_l
#> 32 32 0.2757614 NA
#>
#>
#> DNN solver ended normally after 736 iterations
#>
#> logL:-43.177633 srmr:0.101807
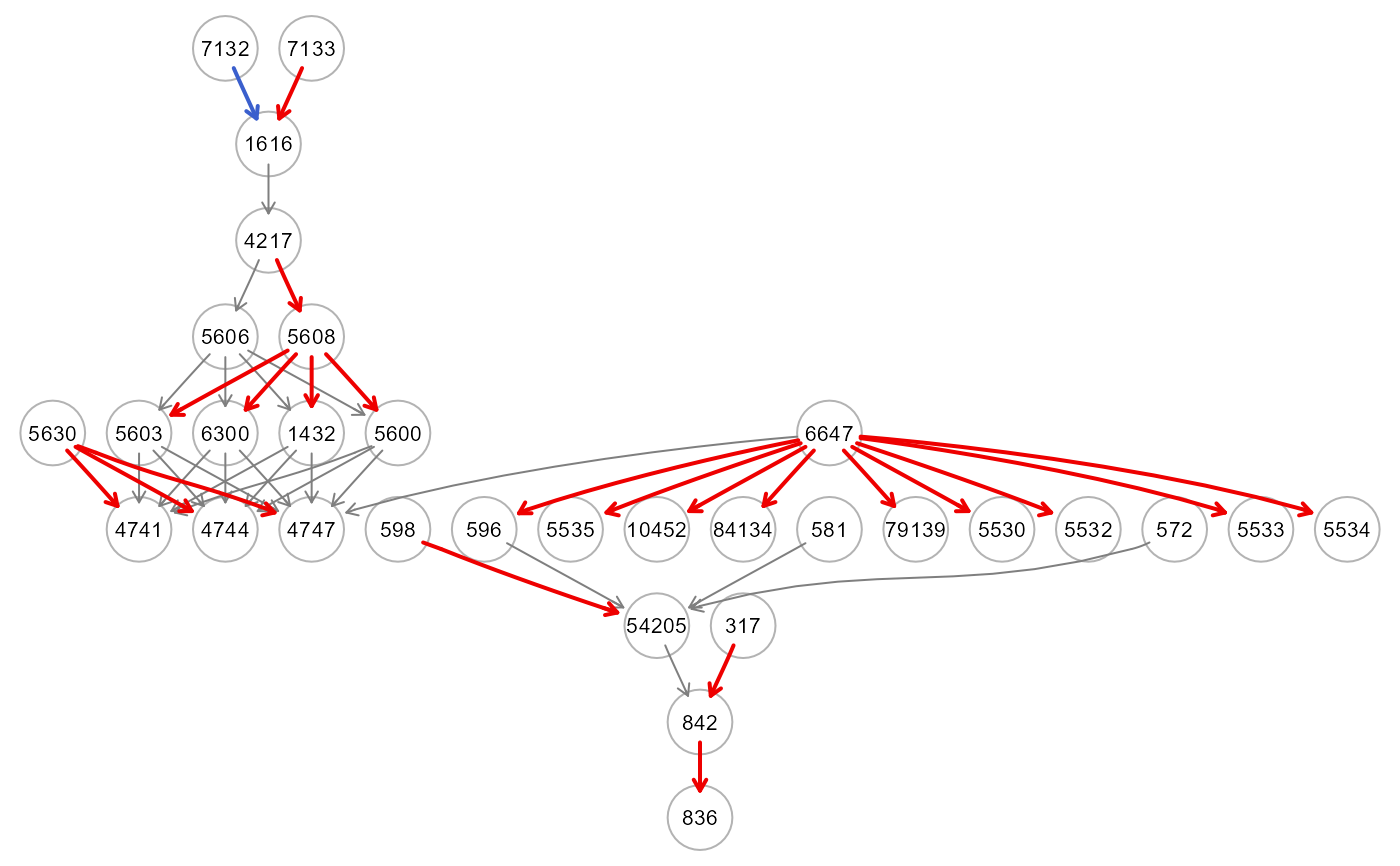 #>
#> gray50 red2 royalblue3
#> 22 19 4
# }
#>
#> gray50 red2 royalblue3
#> 22 19 4
# }